Chapter 5: Planetary Orbits
Chapter Objectives
Upon completion of this chapter you will be able to describe in general terms the characteristics of various types of planetary orbits. You will be able to describe the general concepts and advantages of geosynchronous orbits, polar orbits, walking orbits, Sun-synchronous orbits, and some requirements for achieving them.
Orbital Parameters and Elements
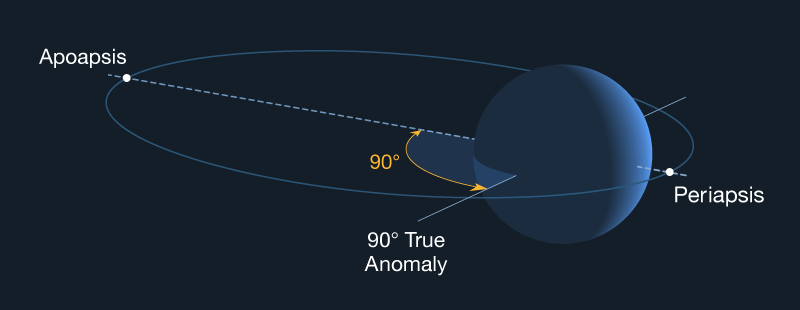
The terms orbital period, periapsis, and apoapsis were introduced in Chapter 3.
The direction a spacecraft or other body travels in orbit can be direct, or prograde, in which the spacecraft moves in the same direction as the planet rotates, or retrograde, going in a direction opposite the planet's rotation.
True anomaly is a term used to describe the locations of various points in an orbit. It is the angular distance of a point in an orbit past the point of periapsis, measured in degrees. For example, a spacecraft might cross a planet's equator at 10° true anomaly.
Nodes are points where an orbit crosses a reference plane, such as the ecliptic or the celestial equator. As an orbiting body crosses the reference plane going north, the node is referred to as the ascending node; going south, it is the descending node.
The reference plane to use in defining the ascending node will depend on what you're doing. If you wish to reference your spacecraft's motion to the body it's orbiting, you would use a plane local to that body: orbiting the Earth you'd use the celestial equator, an extension of the Earth's equatorial plane. Orbiting the Sun you would choose the ecliptic plane, orbiting and studying Venus it would make sense to use an extension of Venus's equatorial plane, etc.
To completely describe an orbit mathematically, six quantities must be calculated. These quantities are called orbital elements, or Keplerian elements, after Johannes Kepler (1571-1630). They are:
- Semi-major axis and
- Eccentricity, which together are the basic measurements of the size and shape of the orbit's ellipse (described in Chapter 3. Recall an eccentricity of zero indicates a circular orbit).
- Inclination is the angular distance of the orbital plane from the plane of the planet's equator (or from the ecliptic plane, if you're talking about heliocentric orbits), stated in degrees. An inclination of 0 degrees means the spacecraft orbits the planet at its equator, and in the same direction as the planet rotates. An inclination of 90 degrees indicates a polar orbit, in which the spacecraft passes over the north and south poles of the planet. An inclination of 180 degrees indicates a retrograde equatorial orbit.
- Argument of periapsis is the argument (angular distance) of the periapsis from the ascending node.
- Time of periapsis passage and
- Celestial longitude of the ascending node are the remaining elements.
The orbital period is of interest to operations, although it is not one of the six Keplerian elements needed to define the orbit.
Generally, three astronomical or radiometric observations of an object in an orbit are enough to pin down all of the above six Keplerian elements. The following table gives a sense of the level of precision an interplanetary mission commonly deals with. These elements are established by analysis of data returned during routine tracking by the Deep Space Network.
Elements of Magellan's Initial Venus Orbit Aug. 10, 1990
1 | Semimajor Axis | 10434.162 km |
2 | Eccentricity | 0.2918967 |
3 | Inclination | 85.69613° |
4 | Argument of Periapsis | 170.10651° |
5 | Periapsis Passage | 1990 DOY 222 19:54 UTC ERT |
6 | Longitude of Ascending Node: | -61.41017° |
Orbit Period | 3.26375 hr |
Types of Orbits
Geosynchronous Orbits
A geosynchronous orbit (GEO) is a prograde, low inclination orbit about Earth having a period of 23 hours 56 minutes 4 seconds. A spacecraft in geosynchronous orbit appears to remain above Earth at a constant longitude, although it may seem to wander north and south. The spacecraft returns to the same point in the sky at the same time each day.
Geostationary Orbits
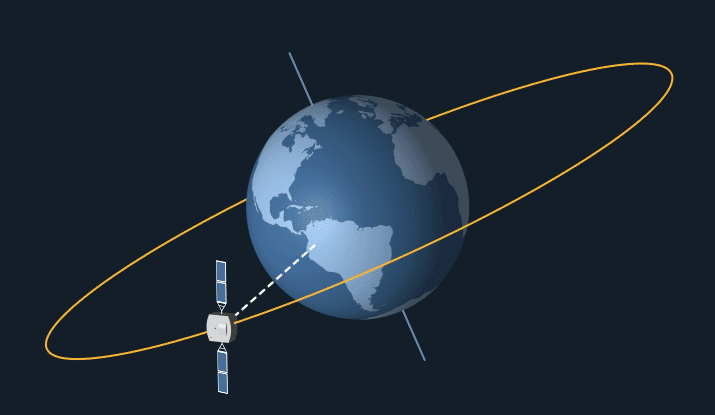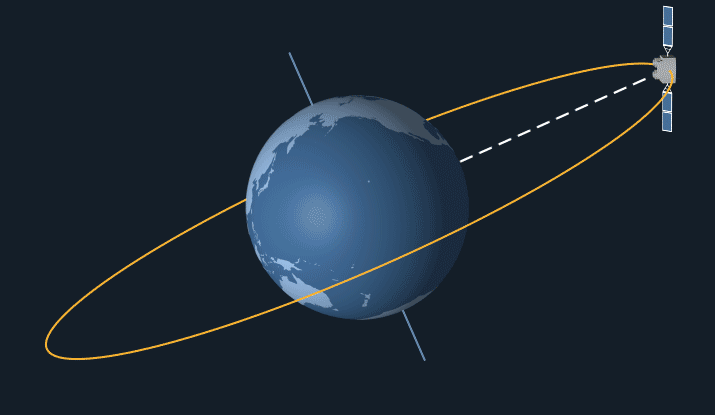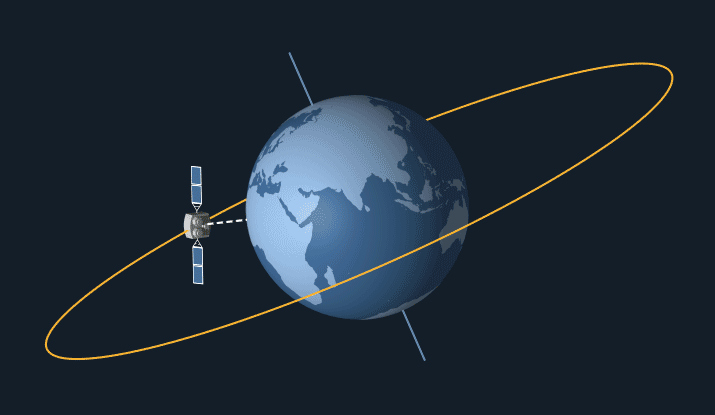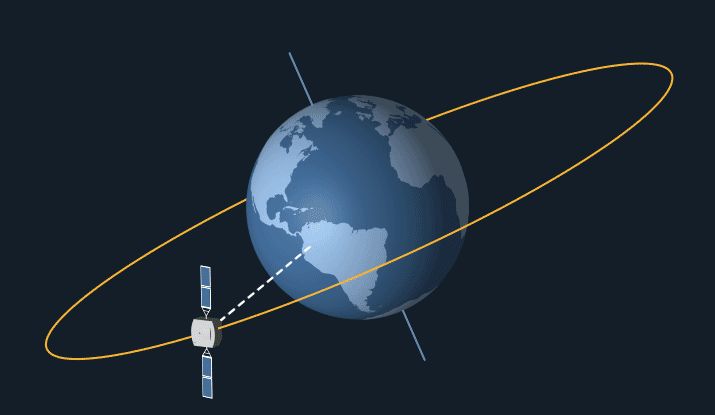
To achieve a geostationary orbit, a geosynchronous orbit is chosen with an eccentricity of zero, and an inclination of either zero, right on the equator, or else low enough that the spacecraft can use propulsive means to constrain the spacecraft's apparent position so it hangs seemingly motionless above a point on Earth. (Any such maneuvering on orbit, or making other adjustments to maintain its orbit, is a process called station keeping.) The orbit can then be called geostationary. This orbit is ideal for certain kinds of communication satellites and meteorological satellites. The idea of a geosynchronous orbit for communications spacecraft was first popularised by science fiction author Sir Arthur C. Clarke in 1945, so it is sometimes called the Clarke orbit.
Geosynchronous Transfer Orbit
To attain geosynchronous (and also geostationary) Earth orbits, a spacecraft is first launched into an elliptical orbit with an apoapsis altitude in the neighborhood of 37,000 km. This is called a Geosynchronous Transfer Orbit (GTO). The spacecraft then circularizes the orbit by turning parallel to the equator at apoapsis and firing its rocket engine. That engine is usually called an apogee motor. It is common to compare various launch vehicles' capabilities according to the amount of mass they can lift to GTO.
Polar Orbits
Polar orbits are 90 degree inclination orbits, useful for spacecraft that carry out mapping or surveillance operations. Since the orbital plane is nominally fixed in inertial space, the planet rotates below a polar orbit, allowing the spacecraft low-altitude access to virtually every point on the surface. The Magellan spacecraft used a nearly-polar orbit at Venus. Each periapsis pass, a swath of mapping data was taken, and the planet rotated so that swaths from consecutive orbits were adjacent to each other. When the planet rotated once, all 360 degrees longitude had been exposed to Magellan's surveillance.
To achieve a polar orbit at Earth requires more energy, thus more propellant, than does a direct orbit of low inclination. To achieve the latter, launch is normally accomplished near the equator, where the rotational speed of the surface contributes a significant part of the final speed required for orbit. A polar orbit will not be able to take advantage of the "free ride" provided by Earth's rotation, and thus the launch vehicle must provide all of the energy for attaining orbital speed.
Walking Orbits
Planets are not perfectly spherical, and they do not have evenly distributed surface mass. Also, they do not exist in a gravity "vacuum." Other bodies such as the Sun, or natural satellites, contribute their gravitational influences to a spacecraft in orbit about a planet. It is possible to choose the parameters of a spacecraft's orbit to take advantage of some or all of these gravitational influences to induce precession, which causes a useful motion of the orbital plane. The result is called a walking orbit or a precessing orbit, since the orbital plane moves slowly with respect to fixed inertial space.
Sun Synchronous Orbits
A walking orbit whose parameters are chosen such that the orbital plane precesses with nearly the same period as the planet's solar orbit period is called a Sun synchronous orbit. In such an orbit, the spacecraft crosses periapsis at about the same local time every orbit.
This can be useful if instruments on board depend on a certain angle of solar illumination on the surface. Mars Global Surveyor's orbit is a 2-pm Mars Local Time Sun-synchronous orbit, chosen to permit well-placed shadows for best viewing.
It may not be possible to rely on use of the gravity field alone to exactly maintain a desired synchronous timing, and occasional propulsive maneuvers may be necessary to adjust the orbit.
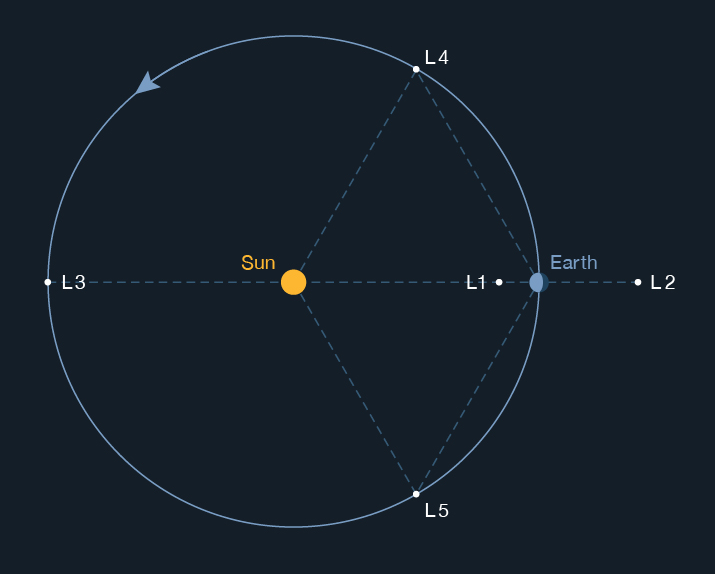
Lagrange points and "Halo" Orbits
Joseph Louis Lagrange (1736-1813) showed how a body of negligible mass (commonly called a "particle," but this can include a spacecraft) could orbit along with a more massive body that is already in a near-circular orbit. In a frame of reference that rotates with the more massive bodies, he found five points at which the combined gravitational forces of the two larger bodies can maintain a particle rotating in a constant relative position as they orbit.
Consider a system with the two massive bodies being the Earth orbiting the Sun. The third body, such as a spacecraft, might occupy any of five Lagrangian points.
In line with the two large bodies are the L1, L2 and L3 points, which are unstable: a spacecraft located there must use its thrusters occasionally to remain near the point.
The leading apex of the triangle is L4; the trailing apex is L5. These last two are also called Trojan points. Natural bodies such as asteroids can often be found at a planet's L4 and/or L5. Trojan moons may also be found orbiting a planet at the planet-moon L4 and L5 points.
With a minimum use of thrusters for stationkeeping, a spacecraft can "orbit" about an unstable Lagrange point. Such an orbit is called a halo orbit because it appears as an ellipse floating over the planet. It is not an orbit in the classical sense, though, since the unstable L point does not exert any attractive force on its own. In the Sun-Earth case for example, the spacecraft's true orbit is around the Sun, with a period equal to Earth's (the year).
Picture a halo orbit as a controlled drift back and forth in the vicinity of the L point while orbiting the Sun. Most of the propulsive stationkeeping maneuvers are executed out near the extremities, or ansas, of the halo, reversing the direction of drift each time by gentle force.
The Solar and Heliospheric Observatory spacecraft (SOHO) follows a "halo" orbit around Earth's L1, which is 1.53 x 106 km from Earth. From there it has an uninterrupted view of its target the Sun, and its orbital excursions ensure that ground stations are not always pointing right at the noisy Sun for communications. The Wilkinson Microwave Anisotropy Probe WMAP spacecraft resides in a halo orbit near Earth's L2 (about the same distance from Earth as L1), where it enjoys an uninterrupted view into deep space. Its 6-month orbit about L2 prevents Earth's shadow from ever blocking the craft's solar arrays. View this movie of WMAP's flight.