Chapter 3: Gravity & Mechanics
Page One | Page Two | Page Three | Page Four
Upon completion of this chapter you will be able to describe the force of gravity, characteristics of ellipses, and the concepts of Newton's principles of mechanics. You will be able to recognize acceleration in orbit and explain Kepler's laws in general terms. You will be able to describe tidal effect and how it is important in planetary systems.
Gravitation is the mutual attraction of all masses in the universe. Since its effect decreases in proportion to distance squared, it never quite disappears completely. Because of this, it applies, to some extent, regardless of the sizes of the masses or their distance apart.
The concepts associated with planetary motions developed by Johannes Kepler (1571-1630) describe the positions and motions of objects in our solar system. Isaac Newton (1643-1727) later explained why Kepler's laws worked, by showing they depend on gravitation. Albert Einstein (1879-1955) posed an explanation of how gravitation works in his General Theory of Relativity.
In any solar system, planetary motions are orbits gravitationally bound to a star. Since orbits are ellipses, a review of ellipses follows.
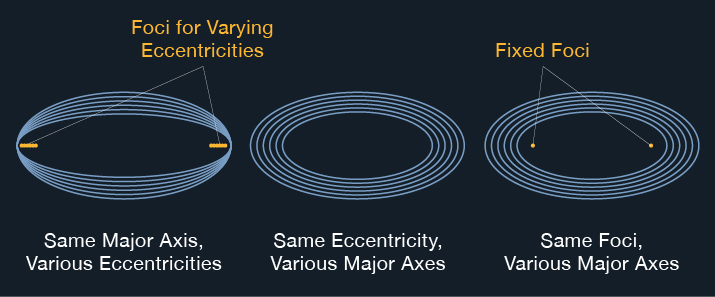
An ellipse is a closed plane curve generated in such a way that the sum of its distances from two fixed points (called the foci) is constant. In the illustration below, the sum of Distance A + Distance B is constant for any point on the curve.
An ellipse results from the intersection of a circular cone and a plane cutting completely though the cone. The maximum diameter is called the major axis. It determines the size of an ellipse. Half the maximum diameter, the distance from the center of the ellipse to one end, is called the semi-major axis.
The shape of an ellipse is determined by how close together the foci are in relation to the major axis.
Eccentricity is the distance between the foci divided by the major axis. If the foci coincide, the ellipse is a circle. Therefore, a circle is an ellipse with an eccentricity of zero.