Basics of Spaceflight: A Gravity Assist Primer
A Gravity Assist Primer
The "gravity assist" concept has proven fundamental to exploring our "back yard" — the solar system. The technique has even been employed at least once to rescue an Earth-orbiting communications satellite whose launch vehicle failed to place it in its intended geosynchronous orbit.
Some History
Several robotic spacecraft have used the "gravity assist" technique to achieve their targets "high up" in the Sun's gravity well. Voyager 2 launched in August 1977 and flew by Jupiter for reconnaissance, and for a trajectory boost to Saturn. Voyager 1 launched the following month and did the same (reaching Jupiter before Voyager 2 did). Voyager 2 then obtained an assist from Saturn and another one later from Uranus, climbing all the way to Neptune and beyond. Galileo took one kick from Venus and two from Earth, while orbiting the Sun en route to its destination, Jupiter. Cassini took two boosts from Venus, one from Earth, and another from Jupiter to gain enough momentum to reach Saturn.
If you find any terms here you don't understand, see the Glossary on Basics of Space Flight, where you can look them up.
Here's Chapter 4, where Gravity Assist, and other trajectories are covered in a little more detail and broader perspective.
The "gravity assist" flyby technique can add or subtract momentum to increase or decrease the energy of a spacecraft's orbit. Generally it has been used in solar orbit, to increase a spacecraft's velocity and propel it outward in the solar system, much farther away from the Sun than its launch vehicle would have been capable of doing. Since a flyby can also decrease a spacecraft's orbital momentum, the Galileo spacecraft decreased its energy, relative to Jupiter, with a gravity assist flyby in front of the Jovian moon Io. In this way, it was possible to decrease the mass of rocket propellant needed for Jupiter orbit insertion. Comets and other bodies in solar orbit naturally experience changes in their orbits once in a while, as they happen to pass close by a planet or a moon.
The two Voyager spacecraft provide a classic example. They were launched aboard a Titan-III/Centaur, with destinations of Saturn and beyond. But their launch vehicles could provide only enough energy to get them to Jupiter (halfway out to Saturn). Had Jupiter not been there at the right time, the spacecraft would have reached aphelion near Jupiter's orbital distance (about 5 AU or 750,000,000 km from the Sun). Their perihelion would have been around Earth's orbital distance (1 AU or 150,000,000 km), and they would have remained in that orbit until a planet or something else caused it to change.
But of course their launch time was planned so that Jupiter coasted by at just the right time. The spacecraft felt Jupiter's gravity and started falling toward it. The spacecraft's velocity brought it close behind Jupiter in its solar orbit, but not close enough to impact. As Voyager climbed "up" away from Jupiter, it slowed down again with respect to Jupiter, eventually reaching the same speed it had on its way in.
How It Works
From Jupiter's point of view, the situation is similar to a bicyclist speeding up going downhill into a valley, then slowing down again on the uphill part of the road.
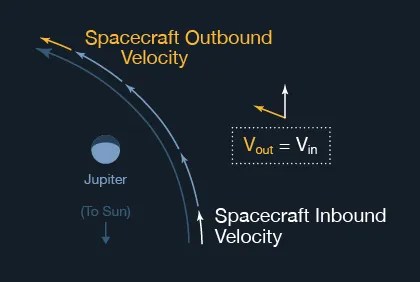
In the vector diagram at left, the situation is simplified to two dimensions. You can see the magnitude and direction of the spacecraft's velocity on its way in towards Jupiter in the lower right. At the upper left, you can see that the accelerating force of Jupiter's gravitation has made a significant change in the direction of the spacecraft's velocity, but not in its magnitude. (These represent velocity at "infinity," from Jupiter, that is, before and after being noticeably changed by Jupiter's presence.) Near the middle of the diagram, the long arrow shows that there's a significant, but temporary, increase in the magnitude (speed). Note these speeds are all with respect to Jupiter.
To look at the same phenomenon in terms of a cyclist, VIN shows the cyclist approaching a downhill grade into a canyon. VOUT shows that the cyclist slowed down again at the top of the ensuing uphill grade (of course this cycling analogy asks us to ignore air friction and vehicle friction, etc., which are virtually absent in the spacecraft's case). Indeed, after negotiating the canyon, the cyclist's direction has changed, but in the end s/he has not made a lasting change in speed (unless you don't ignore all that friction etc.).
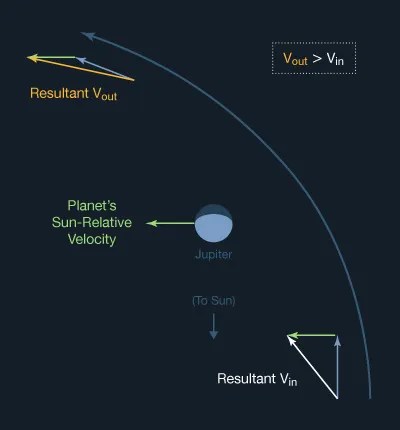
The planet's own motion is a key. A gravity assist with Jupiter involves not a stationary planet as considered above, but a planet with enormous angular momentum as it revolves around the Sun. In the diagram at right, Jupiter's motion along its solar orbit has been illustrated with a vector colored red (simplified, of course: Jupiter revolves along an arc, not a straight line. Imagine the Sun situated below the bottom of the diagram). The spacecraft acquires this Sun-relative vector, or a significant portion of it, during its interaction with Jupiter.
You can see how the red vector is added to VIN and VOUT. The resulting vector shows how the spacecraft's velocity, relative to the Sun, takes on a nice boost from Jupiter. Notice how rotation of the vector from VIN to VOUT (the bending of the spacecraft's path by the planet's gravity) helps increase the result. This trajectory bending is the other key.
The spacecraft is a physical mass, so it has its own gravitation. That's how the spacecraft can tug on Jupiter and actually decrease the planet's orbital momentum by a tiny amount. In the exchange, the spacecraft acquires momentum from Jupiter — a significant amount, compared to the momentum the spacecraft already had.
Some More Analogies
To help make a complicated-sounding concept easily understandable, consider the analogy in baseball. Picture a fast pitch coming toward the batter. The baseball represents a spacecraft. Now picture what the batter does, swinging a bat with all the force s/he can muster. The business end of the bat in motion represents a massive planet like Jupiter. The bat connects with the ball: wham! The ball receives momentum from the bat, and takes off in a different direction with a lot more speed as it soars out of the stadium. Of course in this analogy, the ball interacts with the bat mechanically, rather than by mutual gravitation. (Or you could look even closer and observe the ball's atoms interacting with repulsive electric force with the bat's atoms.) The results are similar: momentum taken from an object that has lots of it, and transferred into an object that makes use of its new-found momentum.
Another analogy, illustrated by the cartoon above, involves a moving railroad train that represents Jupiter, moving along its track about the Sun. The kid in the propeller beanie throws a tennis ball that represents a spacecraft. It encounters the train, which transfers its momentum into the ball.
It's interesting to note the speeds in the cartoon. The propeller-beanie kid sees his tennis ball moving away from him at 30 miles per hour. So does the Sun, sitting on the stationary platform. The engineer driving the train sees the ball coming at about 80 MPH, since the train is moving 50 MPH with respect to the ground. The train and ball interact at 80 MPH. The ball rebounds from the front of the train at nearly the same 80 MPH, which can be added to the 50 MPH speed of the train, because it acquired it from the train. The result approaches a total of 130 MPH. This scenario is analogous the velocity of a spacecraft being added to the velocity of the massive speeding planet, and "rebounding" with a higher velocity still (although the spacecraft's "rebound" is a gravitational, rather than a mechanical, interaction, like in the baseball analogy).