Chapter 3: Gravity & Mechanics
Page One | Page Two | Page Three | Page Four
Sir Isaac Newton realized that the force that makes apples fall to the ground is the same force that makes the planets "fall" around the Sun. Newton had been asked to address the question of why planets move as they do. He established that a force of attraction toward the Sun becomes weaker in proportion to the square of the distance from the Sun.
Newton postulated that the shape of an orbit should be an ellipse. Circular orbits are merely a special case of an ellipse where the foci are coincident. Newton described his work in the Mathematical Principles of Natural Philosophy (often called simply the Principia), which he published in 1685. Newton gave his laws of motion as follows:
- Every body continues in a state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.
- The change of motion (linear momentum) is proportional to the force impressed and is made in the direction of the straight line in which that force is impressed.
- To every action there is always an equal and opposite reaction; or, the mutual actions of two bodies upon each other are always equal, and act in opposite directions.
(Notice that Newton's laws describe the behavior of inertia, they do not explain what the nature of inertia is. This is still a valid question in physics, as is the nature of mass.)
There are three ways to modify the momentum of a body. The mass can be changed, the velocity can be changed (acceleration), or both.

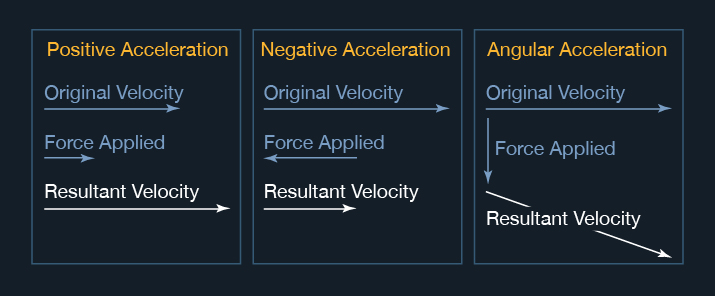
Acceleration may be produced by applying a force to a mass (such as a spacecraft).
If applied in the same direction as an object's velocity, the object's velocity increases in relation to an unaccelerated observer.
If acceleration is produced by applying a force in the opposite direction from the object's original velocity, it will slow down relative to an unaccelerated observer. If the acceleration is produced by a force at some other angle to the velocity, the object will be deflected. These cases are illustrated below.

The world standard of mass is the kilogram, whose definition is based on the mass of a metal cylinder kept in France. Previously, the standard was based upon the mass of one cubic centimeter of water being one gram, which is approximately correct. The standard unit of force is the newton, which is the force required to accelerate a 1-kg mass 1 m/sec2 (one meter per second per second). A newton is equal to the force from the weight of about 100 g of water in Earth's gravity. That's about half a cup. A dyne is the force required to accelerate a 1-g mass 1 cm/s2.
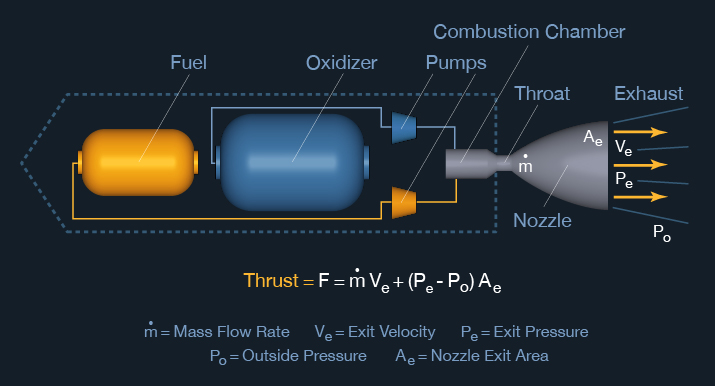
A rocket provides the means to accelerate a spacecraft. Like an airplane's jet engine, a rocket creates thrust by expelling mass to take advantage of Sir Isaac Newton's third law (see above). In both systems, combustion increases the temperature of gas in the engine, whereupon it expands and rushes out through a nozzle. The vehicle is accelerated in the opposite direction.
Where a jet engine on an airplane obtains its oxidizer for combustion directly from the atmosphere, a rocket carries its own oxidizer and can operate outside the atmosphere. Otherwise, their basic operating principle is the same.
The space shuttle main engines, and the Vulcain engine in the Ariane 5 launch vehicle, and many others, all use water as the reaction mass, as does a water-bottle rocket. In launch vehicle engines, the water in its gaseous state because it is hot from the combustion process that freshly created it by burning hydrogen with oxygen. This combustion energy (instead of the limited air pressure in a water-bottle rocket) expands and greatly accelerates the reaction mass out the nozzle, propelling the rocket forward.
The reaction mass is not always water. The nature of the exiting mass depends on the chemistry of the propellant(s). Solid-propellant rockets have been used for centuries, operating on the same basic principle, but with different reaction mass and combustion chemistry. Today they are used as strap-on boosters for liquid-fuel launch vehicles, for orbit injection stages, and for many standalone rockets. Modern solid rockets have a core of propellant made of a mixture of fuel and oxidizer in solid form held together by a binder. The solid is molded into a shape having a hollow core that serves as the combustion chamber. Once ignited, a solid rocket cannot be shut off.
The first flight of a liquid-propellant rocket was in 1926 when American professor Robert H. Goddard launched a rocket that used liquid oxygen and gasoline as propellants. It gained 41 feet during a 2.5-second flight. Liquid propellants have the advantage of fairly high density, so the volume and mass of the propellant tanks can be relatively low, resulting in a high mass ratio. Liquid rockets, once started, can be shut off. Some kinds can later be restarted in flight.

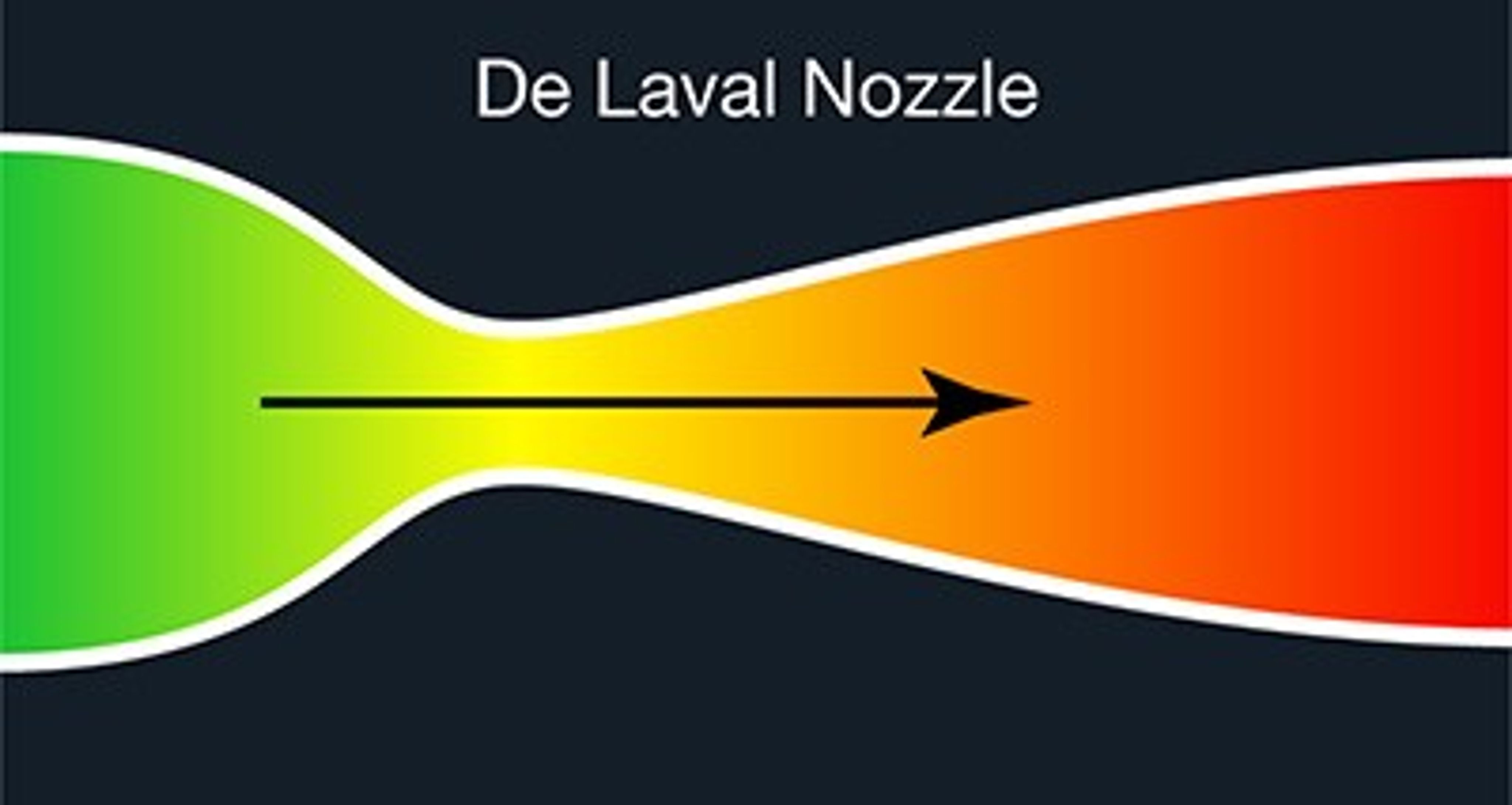
An essential part of the modern rocket engine is the convergent-divergent nozzle (CD nozzle) developed by the Swedish inventor Gustaf de Laval in the 19th century who was working to develop a more efficient steam engine.
Its operation relies on the different properties of gases flowing at subsonic and supersonic speeds. The speed of a subsonic flow of gas will increase where the conduit carrying it narrows. At subsonic flow the gas is compressible; Near the nozzle "throat", where the cross sectional area is a minimum, the gas velocity becomes transonic (Mach number = 1.0), a condition called choked flow. As the nozzle cross sectional area increases the gas expands, its speed increases to supersonic velocities, and pressure waves cannot propagate backwards. This nozzle design was key to Goddard, whose engine achieved energy conversion efficiencies of up to 63% - more efficient than any heat-based engine at the time - making space flight a real possibility.
Here is a link to a thorough discussion of Rocket-Propulsion Basics, including various types of liquid and solid rocket engines, as well as rocket staging. Follow this link to the NASA Glenn Research Center for an interactive nozzle design simulator. It allows selection of nozzles for turbine engines or rocket engine, and shows results for various parameter inputs.
The image of “throwing mass” to gain a reaction, as discussed above, illustrates the basis of rocket propulsion, which works according to the natural principle of conservation of momentum.
The Rocket Equation reveals the motion of a vehicle that can accelerate itself by expelling part of its mass. It is also called The Classical Rocket Equation, the Ideal Rocket Equation, and the Tsiolkovsky Rocket Equation. The latter recognizes the work of the Russian-Soviet Konstantin Tsiolkovsky (1857 – 1935) in pioneering astronautic theory.
The faster you can expel mass from the rocket, the faster it can move forward. The Rocket Equation shows this result, in the first term, as change in velocity, starting with the upper-case Greek letter Delta, followed by a lower-case v.
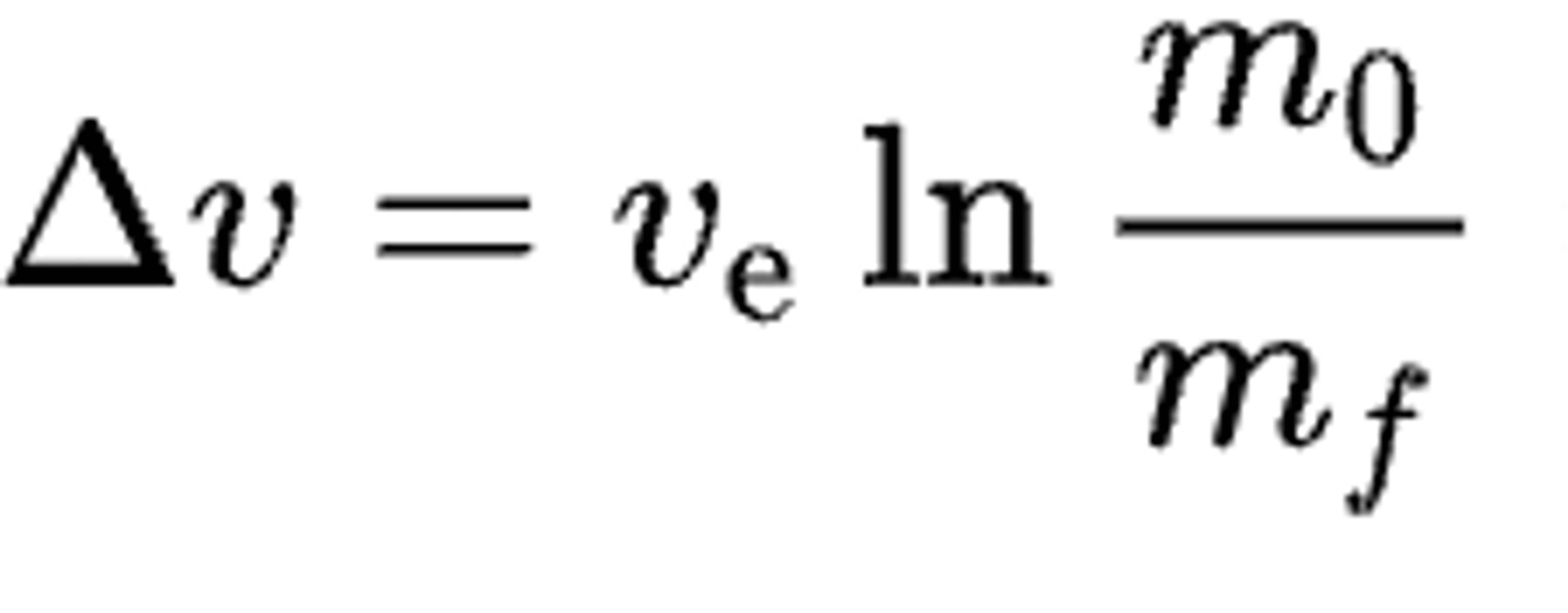
Delta-v is the maximum change of velocity (if there are no external forces acting) that a rocket-powered vehicle can experience by expelling some of its mass.
ve is the effective velocity of the expelled mass, the exhaust velocity. The highest achievable ve today is around 4.5 km/s for liquid-propellant engines, and about 2.5 km/s for solid-propellant rockets. Non-chemical propulsion systems, such as ion engines, can take the figure an order of magnitude higher. Actual velocity may differ from effective velocity if operating under atmospheric pressure, or if a propulsion system bleeds off propellants to run turbopumps.
m0 is the rocket's initial total mass, including propellant, before the propulsion system begins operating.
mf is the final total mass without the spent propellant, after the propulsion system stops operating.
ln is the natural log, base e, sometimes written “loge” (e is the natural constant whose value is about 2.718).
Terms can also be appended to the Rocket Equation expressed above for maximizing performance when operating within an atmosphere. Be sure to see “Perspective: Launch Mass” in Chapter 14. See also Arthur C. Clarke’s 1950 non-fiction book, Interplanetary Flight, which does an excellent job elaborating on the Rocket Equation.
A useful parameter that indicates a particular rocket engine's efficiency is its specific impulse, ISP which is a ratio of the thrust produced to the weight flow of the propellants. It represents the impulse (change in linear momentum) per unit of propellant. The higher the specific impulse, the less propellant is needed to gain a given amount of momentum. ISP is a useful value to compare engines, much the way "miles per gallon" is used for fuel-burning automobiles. A propulsion method with a higher specific impulse is more propellant-efficient. ISP is commonly given in seconds (of time) when it is computed using propellant weight (rather than mass).
Chapter 11 discusses rocket propulsion systems aboard spacecraft, and Chapter 14 shows a variety of launch vehicles.
We learn from Einstein's special theory of relativity that mass, time, and length are variable, and the speed of light is constant. And from general relativity, we know that gravitation and acceleration are equivalent, that light bends in the presence of mass, and that an accelerating mass radiates gravitational waves at the speed of light.
Spacecraft operate at very high velocities compared to velocities we are familiar with in transportation and ballistics here on our planet. Since spacecraft velocities do not approach a significant fraction of the speed of light, Newtonian physics serves well for operating and navigating throughout the solar system. That said, navigational aids such as the fleet of Global Positioning System, GPS, spacecraft do require special-relativity calculations in order to provide accurate position determination. Also, accuracies are routinely enhanced by accounting for tiny relativistic effects. Once we begin to travel between the stars, velocities may be large enough fractions of light speed that Einsteinian physics will be indispensable for determining trajectories.
For now, spacecraft do sometimes carry out experiments to test special relativity effects on moving clocks, and experiments to test general relativity effects such as the space-time warp caused by the Sun, frame-dragging, the equivalence of acceleration and gravitation (more precisely the equivalence between inertial mass and gravitational mass) and the search for direct evidence of gravitational waves.
As of April 2006 there has been no test by which an observer could tell acceleration from gravitation, nor has gravitational radiation been directly observed by a spacecraft. However, the Earth-based Laser-Interferometer Gravitational-Wave Observatory (LIGO), succeeded in making the breakthrough discovery of gravitational radiation from a pair of merging black holes, in February 2016. Some of these subjects are explored in Chapter 8.






